
说到定位算法,一般我们第一个想到的方案就是三边测量法(Trilateration),通过三个信号点(Beacons)和分别对应的距离,形成三个圆并相交于一点。但是实际情况并没有那么理想化,有可能会出现两圆不相交、圆包含圆、只有两个信号点或者多个信号点排成一列的情况(过道里),这都是一些比较常见的场景。所以我们需要一个能同时解决上面这些问题的计算方法——分步定位法。
分步定位法
在iOS开发中,使用CLLocationManager的startRangingBeaconsInRegion:方法监听Beacons,并通过代理回调中获得Beacons列表。取出rssi信号值最强的三个点,取accuracy值作为圆半径(需要减去高度差),用major、minor值从后台返回的数据中取出对应的坐标点数据即为三个圆的圆心。
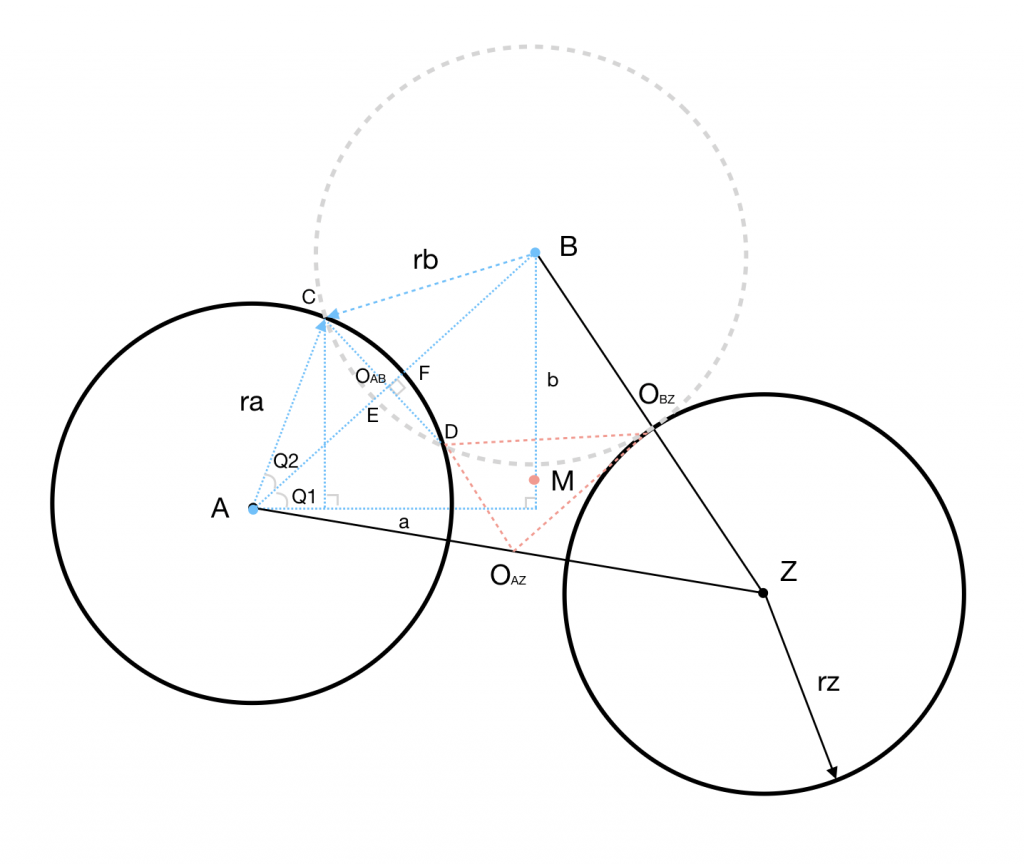
该算法比较简单,如图1-1,不相交时,按比例取中点(OAZ和OBZ)。当两圆相交时,就是拆分成几个三角形,通过一系列三级函数计算出未知的两个交点。最后将三点连成三角形,此三角形的重心(即点M)就是最终定位点,步骤如下:
- 通过勾股定律用a、b长度计算出线段AB长度(即点A到点B距离),使用 ra + rb 与AB对比即可得知两圆的对应情况,一共有三种情况:两圆相离
ra + rb < AB、两圆相切ra + rb == AB、两圆相交ra + rb > AB。 - 两圆相离:按照两圆半径的比例在线段AZ上求OAZ点,即 ra : rz = |AOAZ| : |OAZZ|;“两圆相切”使用“两圆相离”相同的求法即可。
- 两圆相交:求出相交点C的坐标 {Cx, Cy},可通过arccos( a / AB )得出Q1,通过arccos( AOAB / ra )得出Q2,最后计算出点C的坐标:
Cx = Ax + (ra + cos(Q1+Q2))
Cy = Ay + (ra + sin(Q1+Q2))
同理可求出点D的坐标。得到C、D两交点后取距离圆心Z点近的交点作为最后三个参考点中的一点。 - 将最后求得的三个参考点连接成一个三角形,该三角形的重心即为最后的定位点M:
Mx = (Dx + OAZx + OBZx) / 3
My = (Dy + OAZy + OBZy) / 3
采用分步定位法测量一个移动节点的位置,只需要3个参考节点。该定位法还避免了采用三边测量法可能无解的情况,使得该方法的适应性更强。
相关代码
CGPoint pointA = [self sidePointCalculationWith:x1 :y1 :r1
:x2 :y2 :r2
:x3 :y3 ];
CGPoint pointB = [self sidePointCalculationWith:x2 :y2 :r2
:x3 :y3 :r3
:x1 :y1 ];
CGPoint pointC = [self sidePointCalculationWith:x1 :y1 :r1
:x3 :y3 :r3
:x2 :y2 ];
double Mx = (pointA.x + pointB.x + pointC.x) / 3;
double My = (pointA.y + pointB.y + pointC.y) / 3;
-(CGPoint)sidePointCalculationWith:(double)x1 :(double)y1 :(double)r1
:(double)x2 :(double)y2 :(double)r2
:(double)x3 :(double)y3{
//勾股定理 sqrt(X)是X开根号 pow(X,n)是X的n次方
//取beacon1圆心A 与 beacon2圆心B的距离
double AB = sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
double rAB = (r1 + r2);
if (rAB > AB && (r1 < AB && r2 < AB)) {
//两圆有相交点,两圆相交点为C、D。两圆与AB的相交点为E、F。o是EF的中点。
double EF = rAB - AB;
double Eo = EF * 0.5;
double AE = r1 - EF;
double Ao = AE + Eo;
double AQ1 = acos((x2 - x1) / AB);
double AQ2 = acos(Ao / r1);
double BF = r2 - EF;
double Bo = BF + Eo;
// double BQ1 = acos(fabs(x1 - x2) / AB);
double BQ2 = acos(Bo / r2);
//原点{0,0}在左上角的情况下
double Cx = x1 + (r1 * cos(AQ1 + AQ2));
double Cy = 0.0;
double Dx = x2 - (r2 * cos(AQ1 + BQ2));
double Dy = 0.0;
if (x1 < x2) {
Dx = x2 - (r2 * cos(AQ1 + BQ2));
if (y1 < y2) {
Cy = y1 + (r1 * sin(AQ1 + AQ2));
Dy = y2 - (r2 * sin(AQ1 + BQ2));
}else{
Cy = y1 - (r1 * sin(AQ1 + AQ2));
Dy = y2 + (r2 * sin(AQ1 + BQ2));
}
}else{
Cy = y1 + (r1 * sin(AQ1 + AQ2));
if (y1 < y2) {
Dy = y2 - (r2 * sin(AQ1 + BQ2));
}else{
Dy = y2 + (r2 * sin(AQ1 + BQ2));
}
}
double Cc = sqrt(pow(Cx - x3, 2) + pow(Cy - y3, 2));
double Dc = sqrt(pow(Dx - x3, 2) + pow(Dy - y3, 2));
return Cc < Dc ? CGPointMake(Cx, Cy) : CGPointMake(Dx, Dy);
}else{
//两圆无相交点
return [self midpointCalculationWith:x1 :y1 :r1
:x2 :y2 :r2];
}
}
-(CGPoint)midpointCalculationWith:(double)x1 :(double)y1 :(double)r1
:(double)x2 :(double)y2 :(double)r2{
double a = y1 - y2;//竖边
double b = x1 - x2;//横边
double rr = r1 + r2;
double s = r1 / rr;
double x = fabs(x1 - (b * s)) ;
double y = fabs(y1 - (a * s)) ;
return CGPointMake(x, y);
}
参考资料
三边测量法,分步定位法比较
苹果核 – iOS端近场围栏检测(一) ——iBeacon
iOS蓝牙开发之iBeacon篇(二)
—END—